近日UC Berkeley的马毅教授的报告《Deep Networks from First Principle》提供了一种系统性的理论观点。
正如费曼所说「What I cannot create I do not understand」。该工作表明,为了学习到线性划分的样本表示,所有这些常用方法都能够精确推导出来,都是实现该目标所必须的。因此,通过该工作,可以更加直观细致地理解神经网络中的常用方法。
本文整理自该报告的部分内容,原报告链接如下:
https://www.youtube.com/watch?v=z2bQXO2mYPo
深度学习的第一性原理
聚类和分类是两种主要的目标,很多任务都可以归类为将数据划分成不同的部分。马毅教授提出,分类和聚类代表的学习任务,与数据压缩(Compression)有关,而这样的任务,通常是在寻找高维目标的低秩结构,且深度网络能够适应于这样的压缩场景。
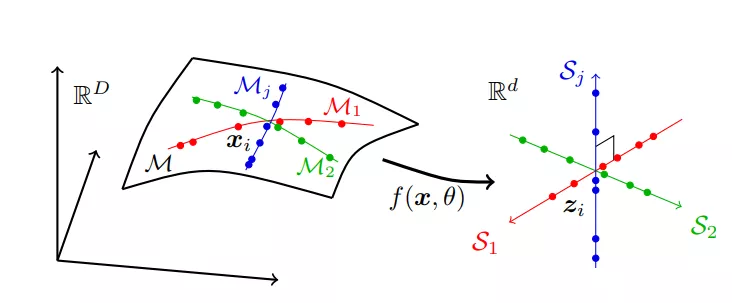
我们引入一个假设,在数据处理中,通常面对的是具有低维结构的高维数据。在这样的情况下,学习的目标通常会包含三个基本问题:
Interpolation,我们寻找样本之间的相似关系,这体现为聚类或分类任务;
Extrapolation,当获得第一个阶段任务的信息后,我们就可以对新的样本进行归类,判断未知样本的结构。
Representation,我们能够了解数据的信息,并建模描述它。
深度学习则将上述数据分析的任务“塞”进黑箱运算中。例如在神经网络分类任务中,我们将输入与输出的标签相互对应,然而足够大的深度网络能够拟合任何给定标签。
尽管在实践中取得了很好的效果,但是理论上来说,训练深度神经网络并不能保证稳定和最优,且我们无法从中了解到模型究竟学到了什么。
IB Theory 提供了一种理解方法,但是,从信息视角理解网络会碰到一个问题,即在高维数据上,传统信息论的统计量是无法定义的,高维数据常常是退化分布的,无法完成有效测量。
通过压缩来聚类和分类
传统聚类方法通常采用最大化相似度的方法进行,而应用在高维退化分布的数据上时,相似度难以定义。因此,我们从更基础的问题出发,为什么需要聚类划分数据?
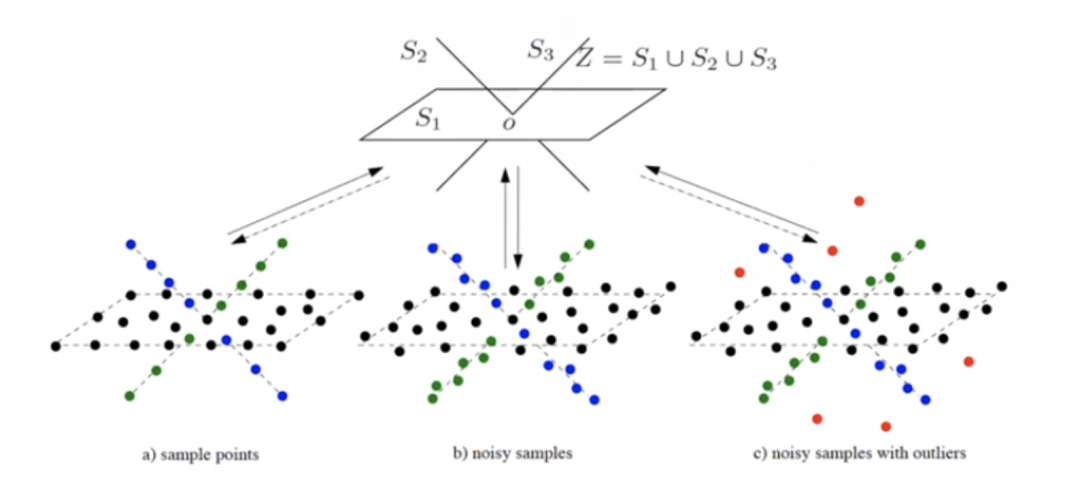
从压缩角度,我们可以看出,能够划分的数据具有更小的空间,通过划分能够获得对数据更有效的表示。如果能找到编码长度的有效度量,就可以设计相应的优化目标。
熵是度量编码长度的工具,但在高维数据上,熵的测量非常困难,马毅教授采用率失真理论来度量这样的表示,提出了编码长度函数(Coding Length Function):
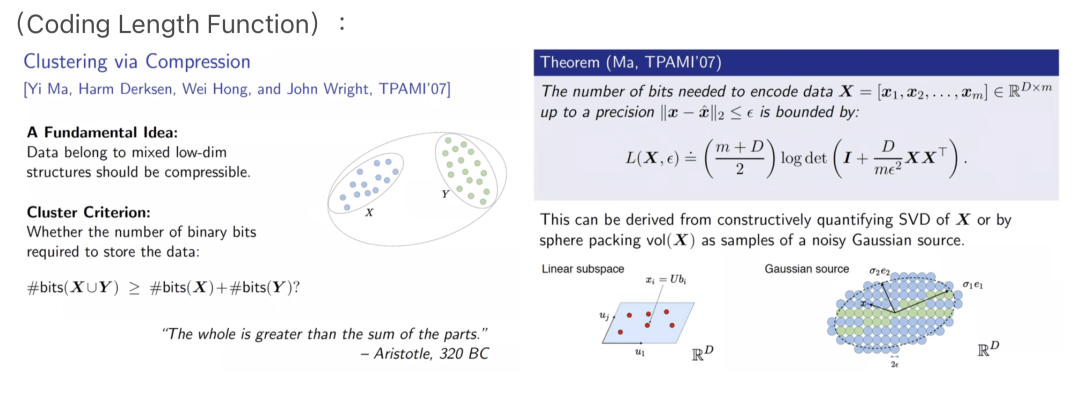
有上图的度量后,我们就能描述聚类或划分的现象,即划分前的数据所须的编码长度,大于划分后的编码长度。这样的划分不需要标签,而是可以通过一些贪心算法,比较不同划分之间的编码长度,获得使划分后编码长度最小的划分。结果展现了这样的方法有非常好的聚类效果,能够找到全局最优的划分,并对离群点非常鲁棒。
同样的方法可以应用于分类任务,通过比较将新数据划分到不同类别增加的编码长度,选取使编码长度增加最少的类别,作为该样本最合适的分类,这种方法依旧来源于最小划分后编码长度的理论。这种方法可以理解为,将新样本划分到合适的类别分类后,所带来的存储开销应当最少,通过正确分类,可以得到最优的表示效率。结果显示,比较传统方法,MICL能够找到更加紧的边界,并且与分类不同的是,其决策边界更接近于数据本身的结构特征。
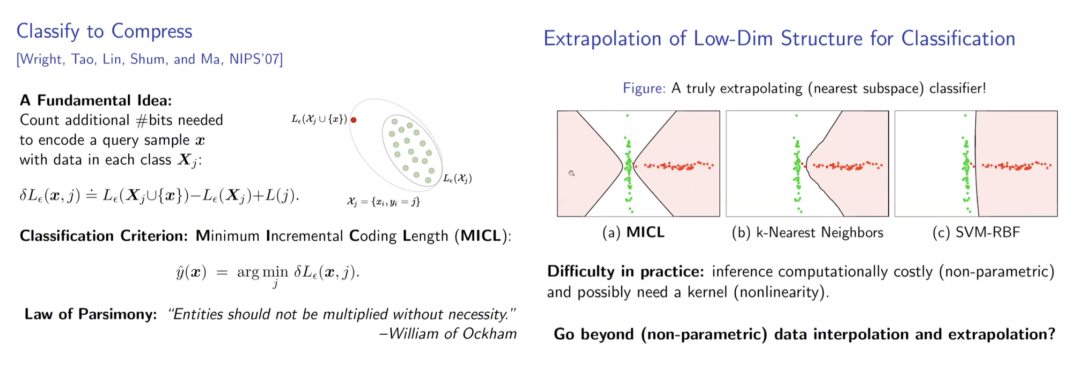
通过最大编码率降低来表示
在完成了 Interpolation(聚类)与 Extrapolation(分类)后,从压缩的视角,还能够实现对数据的表示。当数据符合某种低秩结构时,优秀的表达的目标可以被理解为,最大限度地学习到该结构特征,即,在让同一结构样本靠近的同时,使样本表达能力最大;同时,将不同结构数据间的差异尽可能清晰地体现出来。
具体来说,有三条原则:
1. 压缩同类别数据;
2. 区分不同类别数据;
3. 每类数据能够表达的范围尽可能大。
上文中的Coding Length Function同样为最优表达提供了度量。当样本表达最优时,其表达所占的空间能够最大化,即整体的样本集拥有最大的编码长度。而对于混合类别的数据,令其划分后所须的编码长度最小化,即使其能够让属于不同结构的样本相互靠近。基于这样的目标,CLF描述了如下的学习目标。

这被称为Maximum Coding Rate Reduction (
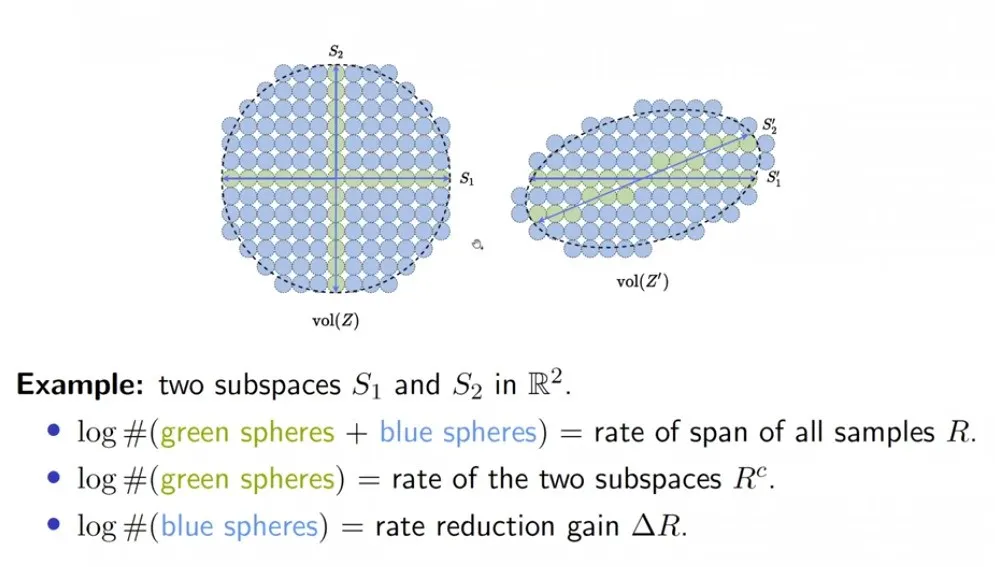
为了使不同范围的样本进行比较,针对每个样本需要进行归一化操作。这与归一化的通常理解相符,使模型能够比较不同范围的样本。
引言
从优化编码率降低来构建深度网络
通过对
而观察E、C两个操作矩阵,会发现其与样本乘积的结果天然带有几何的解释,即样本Z对于其余样本,和各划分类别样本的残差。因此,若需要扩展样本空间的大小,只需加上E与样本相乘获得的残差,若要压缩各类别子空间的大小,仅需减去与C进行相同操作的结果。
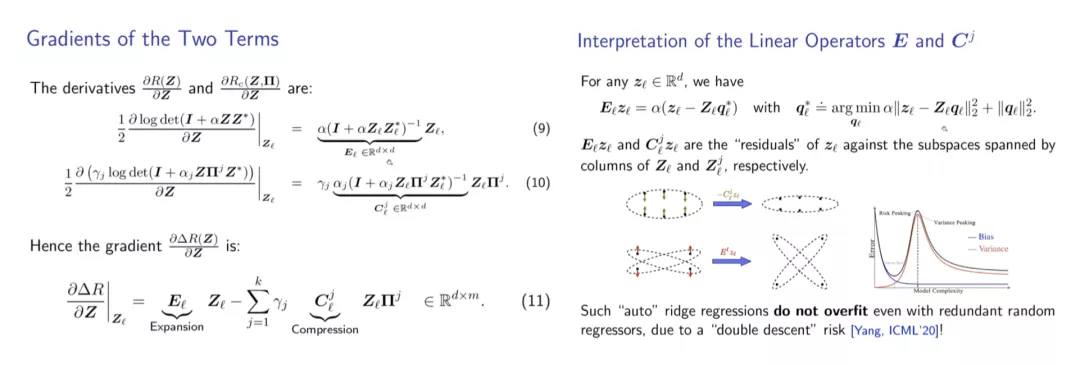
梯度下降过程可以表现为如下结构的网络,其中,每个C对应一个划分的类别,E为求梯度得到的扩张操作矩阵,而梯度下降的更新过程体现为原样本加上得到的梯度,即梯度加上原样本的残差I:
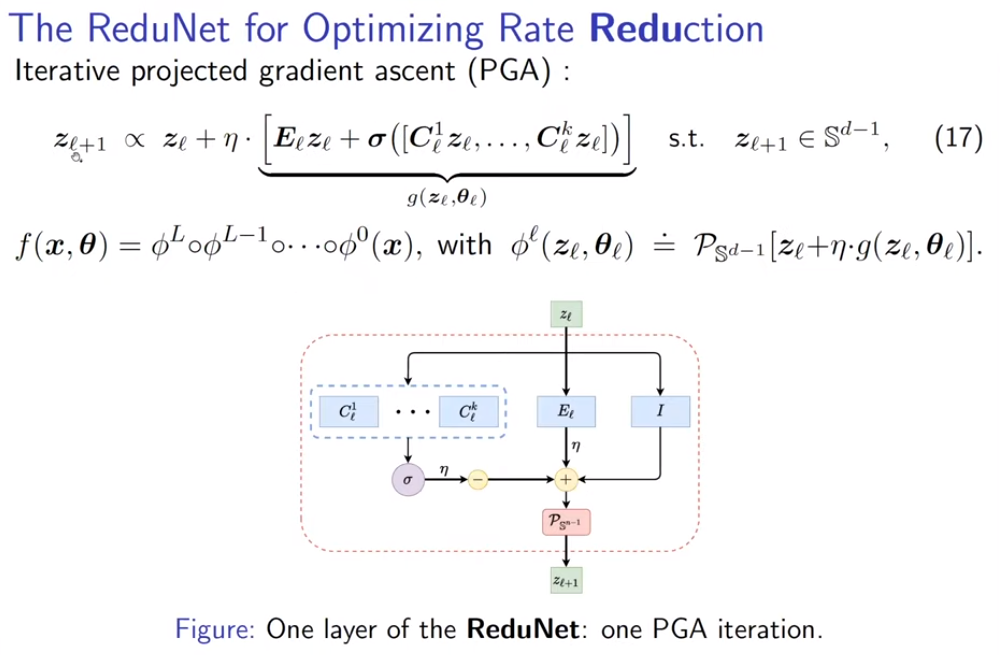
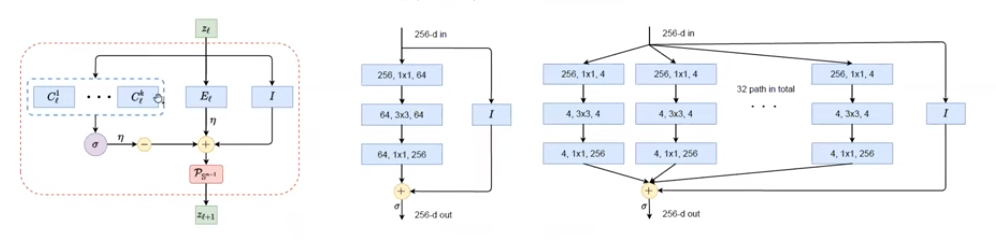
对比常用的神经网络结构,可以发现其与ReduNet有许多相似之处,例如残差链接,C的多通道性质,非线性层等。同时,ReduNet所有参数均能够在前向传播中计算得到,因此网络无需BP优化。
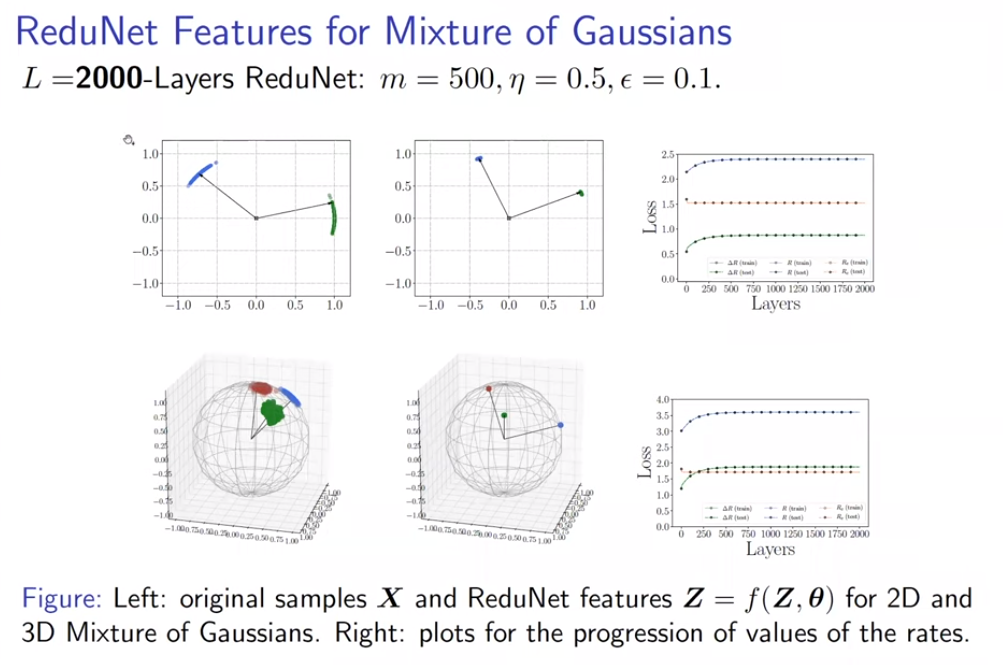
从平移不变性得到卷积网络
通过引入组不变性,将cyclic shift后的样本视为同一组,每次将一组样本编码到不同低秩空间,ReduNet可以实现识别的平移不变性。
同时,类似卷积的网络性质也随之而来。在引入平移不变的任务要求后,网络使用循环矩阵表示样本,因而在与E,C矩阵进行矩阵乘时,网络的操作自然地等价于循环卷积。
但考虑不变性时,另一个问题出现了。当存在无数种shift可能时,若样本是稠密的,则其可以通过变换生成任意信号,因此,样本的稀疏性和不变性是不可兼得的,这体现为“不变性”与“稀疏性”的Trade-off。通常深度网络可能隐含了样本的稀疏化过程,而ReduNet则使用了随机卷积核提取样本的稀疏编码。
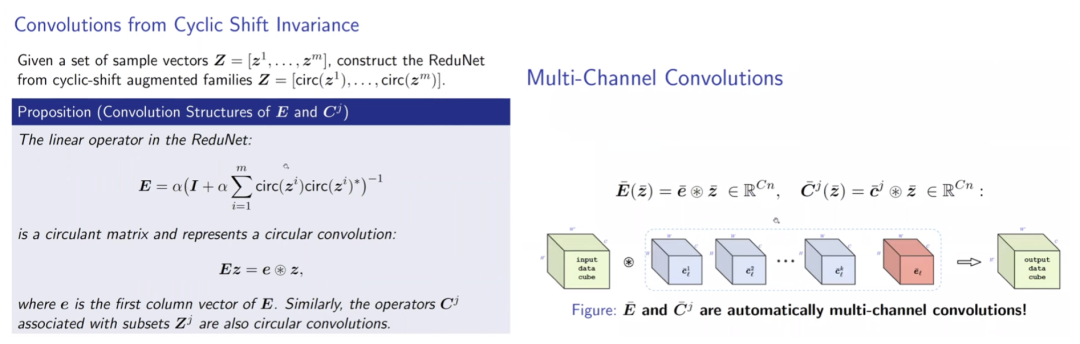
可以看到E,C在考虑不变性后,自动产生了卷积效果,且求逆计算使得通道间的操作相互关联。上述计算还可以通过频域变换来加速计算效率。
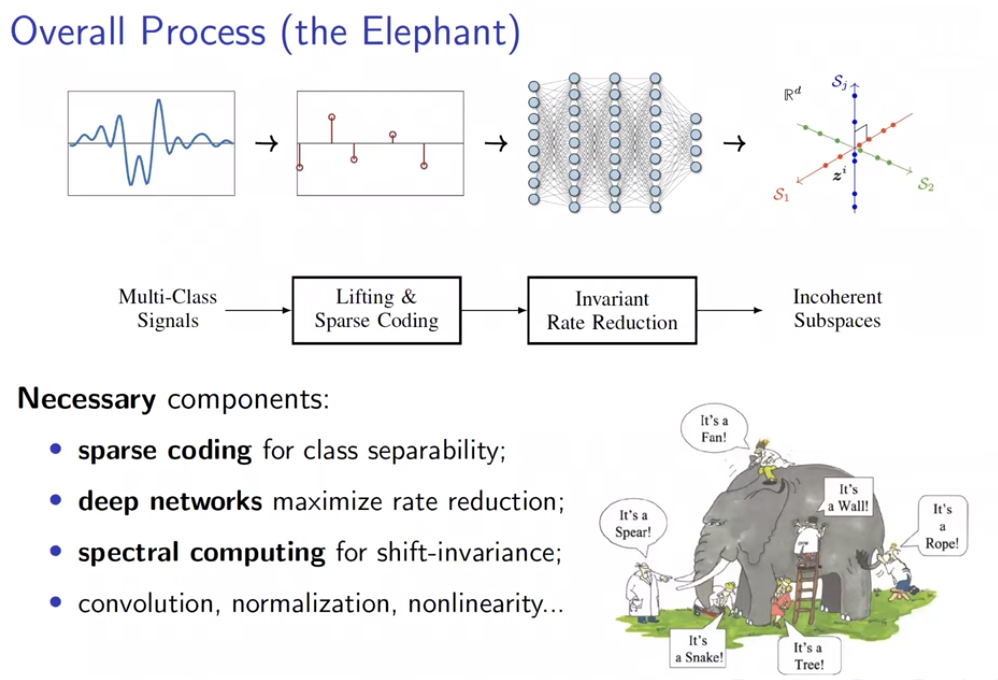

构造的ReduNet也可以通过反向传播训练,且前向传播计算得到的参数,为反向传播训练提供了非常好的参数初始化,通过该初始化得到的参数,经过BP训练后,结果比随机初始化并BP训练的结果有显著提升
马毅教授指出,在构造ReduNet的过程中发现,深度神经网络中常用的操作,稀疏编码,频域计算,卷积,归一化,非线性等等,都是为了实现优化
总结
基于“First Principle”的理论,报告中的工作展现了广泛的前景。报告中拓展了许多未来方向,其中包括基础的关于压缩与学习关联的理论,关于

尽管上文中算法有诸多变化,其核心都是基于“压缩”的概念。
聚类,划分,表征,这些学习任务都可以被表述成压缩任务。我们希望学习到样本的知识,是期望能够更高效地表示样本,因此我们学习类别,提取特征,抽象概念。

转载自:AI科技评论微信公众号


 联系电话
联系电话028-61830850
邮箱:
zjlhbj@uestc.edu.cn
地址:
四川省成都市高新西区西源大道2006号
电子科技大学清水河校区创新中心
版权所有©2020 人机智能技术与系统教育部工程研究中心 蜀ICP备2022017640号-1 公网安备 52032102000193号
